[Data Science] 2. 이상치 탐지(Density Based Anomaly Detection)
2. Density Based Anomaly Detection
💡 Data Science
강필성 교수님의 강의를 보고 정리하였습니다.
이론적 배경
이상치 데이터란
이상치 데이터는 노이즈 데이터와 다름 (노이즈는 어찌할 수 없는 데이터로 측정 과정에서의 무작위성에 기반)
하지만, 이상치 데이터는 정상적인 데이터를 생성하는 매커니즘을 위반하여 생성되는 데이터로 적지만 중요한 데이터
이상치 탐지 사례
Preventive Maintenance
충분하게 수집된 데이터의 대부분은 정상적인 과정(양품을 생산하는 과정) 속에서 수집된 데이터로 불량품이 생성되는 과정 속에서 수집된 데이터(이상치 데이터)는 극소수 → 범주의 불균형이 극심한 상황에서는 분류같은 알고리즘을 적용하기 어렵기 때문에 정상 데이터만을 가지고 학습한 뒤 새로운 데이터가 들어왔을 때 정상 데이터인지 이상치 데이터인지 판별
적용 분야
대부분의 데이터가 한 범주에 속하며 극소수의 데이터만 다른 범주에 속하는 문제 (ex, 제조업 공정에서의 불량 탐지, 신용카드 사기 거래, 통신망의 불법적인 사용 등)

일반화(Generalization)와 특수화(Specialization)
일반화(Generalization) : 주어진 데이터로부터 정상 범주의 개념을 확장해 가는 것
특수화(Specialization) : 주어진 데이터로부터 정상 범주의 개념을 좁혀 가는 것
일반화에 치중할 경우 이상치 데이터 판별이 어렵게 되고 특수화에 치중할 경우 과적합의 위험에 빠질 수 있음

접근 방법
주어진 데이터에는 다수의 정상 데이터와 매우 적은 수의 비정상 데이터가 혼재되어 있음
이상치 탐지는 다수(정상 데이터)만을 사용


평가 지표
이상치 알고리즘에 대한 결과물이 산출되면 이를 바탕으로 최종적으로는 이상치인기 아닌지에 대한 판별을 해야 함
실제 데이터에서는 이러한 cut-off에 따라 정오 행렬이 달라지기 때문에 cut-off에 영향을 받지않는 성능 평가 지표 필요

-
False Regection Rate (FRR) : 원래는 정상이나 이상치 탐지 모델에 의해 이상치로 잘못 판별된 비율
\[PRR=\frac{FP}{FP+TN}\] -
False Acceptance Rate(FAP) : 원래는 이상치라서 탐지가 되어야 하나 모델에 의해 탐지가 되지 못하고 정상으로 판별된 비율
\[FAR=\frac{FN}{TP+FN}\]
이상치 탐지 방법론 평가 지표 그래프

-
Integrated Error : FRR - FAR 그래프 밑면의 넓이 = $1-AUROC$
-
Equal Error Rate (ERR) : FRR과 FAR이 같아지는 지점
ex. ERR = 10%(0.1) → 정상 데이터 10건 중 1건이 이상치로 잘못 판별되거나 이상치 데이터 10건 중 1건이 정상 데이터로 잘못 판별됨을 뜻함
밀도 기반 이상치 탐지
밀도 기반 이상치 탐지 기법
이상치 데이터 정의
- 생성되는 매커니즘이 다른 데이터
- 이상치 데이터가 가진 실제 밀도는 매우 낮음 → 밀도 기반 이상치 탐지 기법의 접근 방식

Low Density Regions는 현재 데이터의 평균과 분산으로 구성된 가오시안 분포에서는 생성될 수 없는 (매우 낮은 확률) 데이터 → 정상이 아닐 것으로 판단
종류
- Gaussian Density Estimation
- Mixture of Gaussian Density Estimation
- Kernel Density Estimation

Gaussian Density Estimation
모든 데이터가 하나의 가우시안(정규) 분포로부터 생성됨을 가정
학습 : 주어진 정상 데이터들을 통해 가우시안 분포의 평균 벡터와 공분산 행렬을 추정
테스트 : 새로운 데이터에 대하여 생성 확률을 구하고 이 확률이 낮을수록 이상치에 가까운 것으로 판단
장점 : 추정이 간단하며 학습시간이 짧음, 적절한 기준치(cut-off)의 분포로부터 정할 수 있음, 각 변수의 측정 단위에 영향을 받지 않음
\[p(\mathbf x)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp [\frac{1}{2}(\mathbf x-\mu)^T\Sigma^{-1}(\mathbf x-\mu)]\]추정해야 하는 파라미터는 $\mu, \sigma^2(\Sigma)$ → 정상 데이터 생성 확률을 최대화 하도록 평균과 분산을 계산하는 것이 가능
\[L=\prod_{i=1}^N P(x_i|\mu, \sigma^2)=\prod_{i=1}^N\frac{1}{\sqrt{2\pi}\sigma}\exp\Big(-\frac{(x_i-\mu)^2}{2\sigma^2}\Big)\\ \log L=-\frac{1}{2}\sum_{i=1}^N\frac{(x_i-\mu)^2}{\sigma^2}-\frac{N}{2}\log(2\pi\sigma^2)\]최대 우도 추정법을 이용하여 해를 찾을 수 있음($\gamma = \frac{1}{\sigma^2}$)
\[\log L=-\frac{1}{2}\sum_{i=1}^N\gamma(x_i-\mu)^2-\frac{N}{2}\log(2\pi)+\frac{N}{2}\log(\gamma)\\ \frac{\partial \log L}{\partial \mu}=\gamma\sum_{i=1}^N(x_i-\mu)=0 \rightarrow \mu=\frac{1}{N}\sum_{i=1}^nx_i\\ \frac{\partial \log L}{\partial \gamma}=-\frac{1}{2}\sum_{i=1}^N(x_i-\mu)^2+\frac{N}{2\gamma}=0 \rightarrow \sigma ^2=\frac{1}{N}\sum_{i=1}^n(x_i-\mu)^2\\\]↳ 일반적인 다변량 데이터에 대해서도 동일한 방식으로 평균 벡터와 공분산 행렬을 구하는 것이 가능
\[\mu=\frac{1}{N}\sum_{i=1}^N\mathbf x_i \quad \quad \quad \Sigma =\frac{1}{N}\sum_{i=1}^N(\mathbf x_i-\mu)(\mathbf x_i-\mu)^T\]하지만 $x \in R^d$일 경우 공분산 행렬은 $d\times d$로 역행렬을 계산하기 어렵거나 존재하지 않을 수 있음

Mixture of Gaussian (MoG) Density Estimation
Gaussian Density Esimation은 데이터 분포에 대해 매우 강한 가정(Unimodal Gaussian)을 가지고 있음
MoG는 데이터가 여러 개의 가우시안 분포의 혼합으로 이루어져 있음을 허용하고 이 가우시안 분포들의 선형 결합으로 전체 데이터 분포 표현

-
하나의 객체가 정상 영역에 속할 확률
\[p(\mathbf x|\lambda)=\sum_{i=1}^M w_mg(\mathbf x|\boldsymbol{\mu} _m, \boldsymbol{\Sigma}_m)\] -
각 가우시안 분포의 밀도 함수
\[g(\mathbf x|\boldsymbol{\mu} _m, \boldsymbol{\Sigma}_m)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp[\frac{1}{2}(\mathbf x -\boldsymbol{\Sigma}_m)^T\sum_m^{-1}(\mathbf x -\boldsymbol{\Sigma}_m)]\\ \lambda=\{w_m,\boldsymbol{\mu}_m, \boldsymbol{\Sigma}_m\}, \quad \quad m=1, \cdots, M\]
Expectation-Maximization Algorithm
- E-step : 주어진 개별 가우시안 분포를 바탕으로 개별 객체가 각 가우시안 분포에 속할 확률을 추정
-
M-step : E-step에서 추정된 확률을 바탕으로 개별 가우시안 분포의 평균, 공분산행렬, 결합 가중치 업데이트
↳ 객체별 가우시안 분포 확률, 개별 가우시안 분포의 평균, 공분산행렬, 결합가중치의 변화가 없을때까지 반복

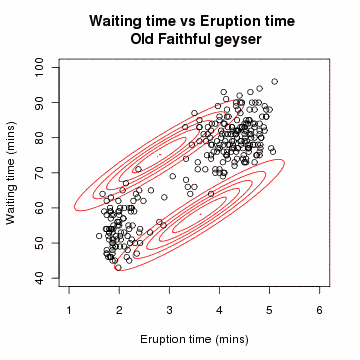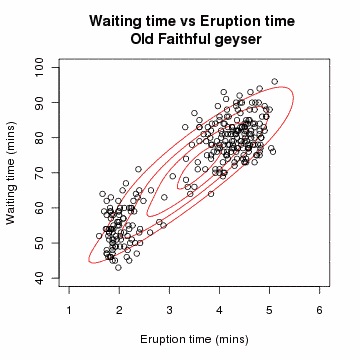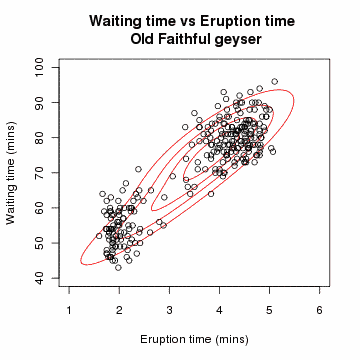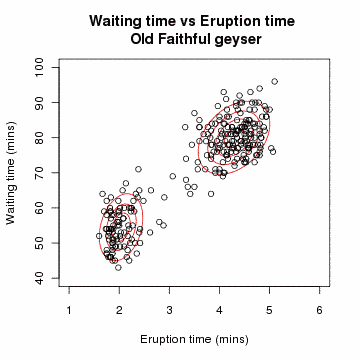
-
Expectation : 각각의 객체들이 $\lambda$라는 개별 파라미터들에 의해 $m$번째 가우시안에 속할 확률
\[p(m|\mathbf x_i, \lambda )=\frac{w_mg(\mathbf x_i|\boldsymbol{\mu}_m,\boldsymbol{\Sigma}_m)}{\sum_{k=1}^M w_k g(\mathbf x_t|\boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)}\] -
Maximization : $p(m\vert\mathbf x_i, \lambda)$ 고정
\[w_m^{(new)}=\frac{1}{N}\sum_{i=1}^Np(m|\mathbf x_i, \lambda)\\ \boldsymbol{\mu}_m^{new}=\frac{\sum_{i=1}^Np(m|\mathbf x_i, \lambda)\mathbf x_i}{\sum_{i=1}^Np(m|\mathbf x_i, \lambda)}\\ \sigma^{2(new)}_{m}=\frac{\sum_{i=1}^Np(m|\mathbf x_i, \lambda)\mathbf x^2}{\sum_{i=1}^Np(m|\mathbf x_i, \lambda)}-\boldsymbol{\mu}^{2(new)}_m\]
공분산 행렬 형태에 따른 MoG 모양

↳ 변수(d)가 매우 크면 Diogonal을 사용하는 것이 안전(full의 역행렬이 생성되지 않아 새로운 데이터가 들어왔을 때, 이상치 스코어 산출이 안될 수 있음)
Kernel-density Estimation
데이터의 특정한 분포를 가정하지 않고 주어진 데이터로부터 주변부의 밀도를 추정하는 방식
과정
확률밀도함수 $p(x)$로부터 생성된 벡터 $x$가 주어진 영역 $R$ 내부에 속할 확률
\[P=\int_R p(x')dx'\]$N$개의 벡터 ${x_1, x_2, \cdots, x_n}$가 동일한 분포로부터 생성되엇을 때 그 중에서 $k$개가 영역 $R$ 내부에 속할 확률
\[P(k)={N \choose k}p^k(1-p)^{N-k}\]이항분포 성질에 의해 $\frac{k}{N}$의 기대값과 분산은
\[E\Big[\frac{k}{N}\Big]=P, \quad Var\Big[\frac{k}{N}\Big]=\frac{P(1-P)}{N}\]$N$이 무한대에 접근하게 되면 위의 식에서 분산은 0에 가까워지고 해당 영역에 대한 발생 확률은 아래와 같음
\[P\cong \frac{k}{N}\]영역 $R$의 크기가 $p(x)$의 변화가 없을 정도로 매우 작다고 가정하면 ($V$는 $R$영역의 Volume)
\[P=\int _R p(x')dx' \cong p(x)V\]위의 두 식을 결합
\[P=\int _R p(x')dx' \cong p(x)V=\frac{k}{N}, \quad p(x)=\frac{k}{NV}\]정리하면 !
\[p(x)=\frac{k}{NV}, \quad where\begin{cases} V : \text{volume surrounding } x\\ N : \text{the total number of examples}\\ k : \text{the number fo examples inside }V \end{cases}\]확률밀도의 추정은 샘플의 수가 클수록, 영역의 볼륨이 작을수록 정확해지지만 실제 상황에서는 데이터의 수는 고정되어 있으므로 적절한 $V$를 찾는 문제로 귀결
(볼륨이 작아야하는 이유는 영역안에서 확률함수값이 변하지 않는다는 가정을 만족시켜야하기 때문, 하지만 너무 작으면 영역안에 데이터가 존재하지 않는 상황이 발생할 수 있음)
→ 영역 $R$ 내부에 충분한 데이터가 포함되도록 크지만 $p(x)$의 변동이 없다는 가정을 뒷받침해줄 수 있도록
위의 식에서 $V$를 고정시키고 $k$를 찾으면 커널 밀도 추정 / 위의 식에서 $k$를 고정시키고 $V$를 찾으면 K-nn

$p(x)=\frac{k}{NV}$로 정의되고 $N=20, \ R=2\times 2$인 정사각형이라고 가정
$R=2\times 2$라는 사각형을 어느 영역에 위치시켰을 때 그 안에 실제 데이터가 몇개 있는지 센 후 밀도함수 추정 → 데이터 상황에 맞게 유연한 확률분포함수 모양을 추정
Parzen Window Density Estimation
$k$개의 객체를 포함하는 영역 $x$를 중심으로 각 면의 길이가 $h$인 Hypercube 정의 (볼륨 $V$는 $h^d$로 정의)

-
kernel function
\[k(u)=\begin{Bmatrix} 1 & |u_j|\lt \frac{1}{2}\quad \forall j=1, \cdots, d \\ 0 & otherwise \end{Bmatrix}\\ k=\sum_{i=1}^N K\Big(\frac{\mathbf x^i-\mathbf x}{h}\Big)\\ p(x)=\frac{1}{Nh^d}\sum_{i=1}^N K\Big(\frac{\mathbf x^i-\mathbf x}{h}\Big)\]
-
$k(u)$의 단점
큐브 가장자리 영역에 의해 0, 1로 나눠지는 불연속적인 추정
$x$를 기준으로 거리가 다름에도 불구하고 Hypercube 내에 있는 객체들에 대한 동등한 가중치
-
-
Smooth kernel function
$k(u)$의 단점을 보완하기 위해 전체 영역에 대한 확률밀도 함수를 1로 표현하면서 smooth한 함수를 사용

-
Smoothing parameter(bandwidth) h

hypercube의 길이인 $h$가 작은 값이면 뾰족한 (spiky) 한 분포를 추정하게 되고 큰 값이면 완만한 분포를 추정
Local Outlier Factor(LOF)
특정 분포를 가정하지 않고 이상치 스코어를 산출할 때, 주변부 데이터의 밀도를 고려

Parzen Window Density Estimation에서는 $k_1 \gt k_2$이기 때문에 $p(x_1)\gt p(x_2)$가 됨 (생성확률이 $x_1$이 더 크기 때문에 anomaly score score은 $x_1$이 작음)
하지만, 여기서 LOF는 문제를 제기!
$x_1$은 밀도가 높은 영역의 중심부이고 $x_2$는 밀도가 낮은 영역의 중심부 → 밀도의 차이이지 중심부라는 것은 동일하기 때문에 $x_1$ anomaly score = $x_2$ anomaly score
LOF score은 주변부 밀도가 높을 때는 중심부에서 조금만 떨어져도 anomaly score는 급격하게 증가하지만 밀도가 낮은 영역에서는 중심부에서 더 많이 떨어져도 anomaly score가 증가하는 폭이 적음
Definition 1 : k-distance of an object p
- 임의의 양의 정수 $k$에 대해서 the k-distance of object p ($k-distance(p)$)는 다음 두 조건 을 만족하는 데이터셋 $D$의 두 점 $p$와 $o$의 거리 $d(p,o)$로 정의됨
- $D$에 속하는 개체 중 $p$를 제외하고 최소한 $k$개의 개체 $o’$ 에 대해서 $𝑑(𝑝,𝑜’)≤𝑑(𝑝,𝑜)$를 만족 → 어떤 $o$라는 기준점이 있을 때, $o$와 $p$(나 자신) 과의 거리보다 더 작거나 같은 $o’$라는 점이 $k$개 있어야 한다
- $D$에 속하는 개체 중 $p$를 제외하고 최대 $k-1$개의 개체 $o’$에 대해서 $𝑑(𝑝,𝑜’) < 𝑑(𝑝,𝑜)$를 만족
- 이는 단순히 동률을 고려한 $k$번째 이웃까지의 거리로 생각할 수 있음

Definition 2 : k-distance neighborhood of an object p
-
개체 $p$의 k-distance가 Definition 1과 같이 주어질 때, k-distance neighborhood of p 는 $p$에서 부터 k-distance보다 멀지 않은 거리에 있는 모든 개체들의 집합을 의미함
\[N_k(p)=\{q\in D\backslash\{p\}|d(p, q)\le k-distance(p) \}\]$p$는 제외한 $q$라는 점들로 구성되어 있고 $p$에서부터 $q$까지의 거리가 $p$의 $k-distance$보다 작거나 같은 점들의 집합

Definition 3 : reachability distance
\[reachability- distance_k(p, o)=\max\{k-distance(o), d(p, o)\}\]
$reachability - distance_3(C, A)$의 경우 $d(C, A)$보다 $3-distance(A)$가 더 크기 때문에 $reachability - distance_3(C, A)=3-distance(A)$
Definition 4 : local reachability density of an object p
\[lrd_k(p)=\frac{|N_k(p)|}{\sum_{o\in N_k(p)}reachability -distance_k(p, o)}\]
- Case 1 : $p$가 $\color{blue}{o}$의 $N_k(p)$에 속함 → $p$는 주변부에 밀도가 높고 집단의 중심부에 위치 → 분모가 작음 → $lrd_k(p)$값 큼
- Case 2 : $p$가 $\color{blue}{o}$의 $N_k(p)$에 속하지 않음 → $p$가 두 개의 높은 밀도를 갖는 군집 사이의 밀도가 낮은 공간에 위치 → 분모가 큼 → $lrd_k(p)$값 작음
Definition 5 : local outlier factor of an object p
\[LOF_k(p)=\frac{\sum_{o\in N_k(p)\frac{lrd_k(o)}{lrd_k(p)}}}{|N_k(p|}=\frac{\frac{1}{lrd_k(p)}\sum_{o\in N_k(p)}lrd_k(o)}{|N_k(p)|}\]
Parzen Window의 경우에는 중심부 영역의 밀도가 case 1에서는 $\frac{5}{NV}$, case 3에서는 $\frac{1}{NV}$로 차이가 나지만 LOF의 관점에서는 anomaly score가 case 1과 case 2에서 비슷하고 case 2의 anomaly score는 높게 나타남

댓글남기기